What is Discrete Structure?
- mathematical structures that can be considered discrete rather than continuous.
The steps for writing proofs.
Axioms - Propositional Logic - Predicate Logic - Rules of Inference - Proof methods - Specific domain knowledge - Proofs
Today I will explain about two steps.
1. Axioms (Gospel Truth)
- Sun is hot.
2. Propositional logic
- Propositional logic is the steps we use to determine the truth of a proposition
- Propositions are statements that we can determine as true or false.
Atomic and Compound Propositions
1. A single proposition may be represented as a propositional variable.
2. An atomic proposition is a single proposition.
3. A compound proposition is a proposition that combines atomic propositions using logical operators.
For example

The one thing have to care about is that these kinds of tautology does not have to be true statement. In this example you can see 15 is divided by 2. It's false. But it is just a stement. You can't judge the statement is True of False.
Logical Operator AND, OR, Exclusive OR, NEGATION
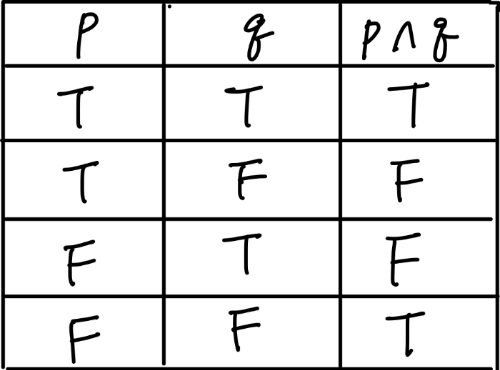
- AND
- A truth table assigns T or F to each proposition and calculates the truth assignment of the entire compund proposition
- Logical And is also called conjunction.
- Given two atomic porpositions, p , q.
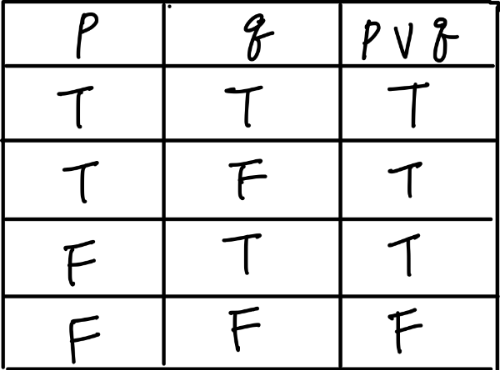
- OR
- A truth table assigns T or F to each proposition and calculates the truth assignment of the entire compund proposition.
- Logical or is also called disjunction
- p, q disjunction table.
- Exclusive OR
- A truth table assigns T or F to each proposition and caculates the truth assignment of the entire compound proposition
- Exclusive OR is true if exactly one of the proposition is true.
- p, q Exclusive OR table

As you can see the both statement is true, Exclusive OR is false
For example, p = Coca Cola is soda pop(T), q = 3 is prime(T) -> Two True = False
p = Diet Coke have calories(F), q = 3 is prime(T) -> One True = True
- Negation
- Observe either a proposition is true of its negation is true
- negation and double negation

For example, p = All primes are odd. Negation of p = There is a primes that is not odd.
Counter : 2 is odd and prime.
'코딩 > Discrete Structures' 카테고리의 다른 글
| Discrete Structure (1) - proposition and consistent system (0) | 2022.09.27 |
|---|